by ANNA HUCULAK (Predictive Solutions)

Table 1. Ergebnis der Zuverlässigkeitsanalyse
Cronbachs Alpha kann Werte zwischen 0 und 1 annehmen, je höher der Wert, desto besser. In unserem Fall ist der Wert von Cronbachs Alpha zufriedenstellend. Ich schlage jedoch vor, es nicht dabei zu belassen, sondern die Zuverlässigkeitsanalyse zu vertiefen. Es ist eine gute Praxis, vor der Erstellung einer Skala zu prüfen, wie sich das Entfernen einzelner Items aus der Skala auswirken würde.
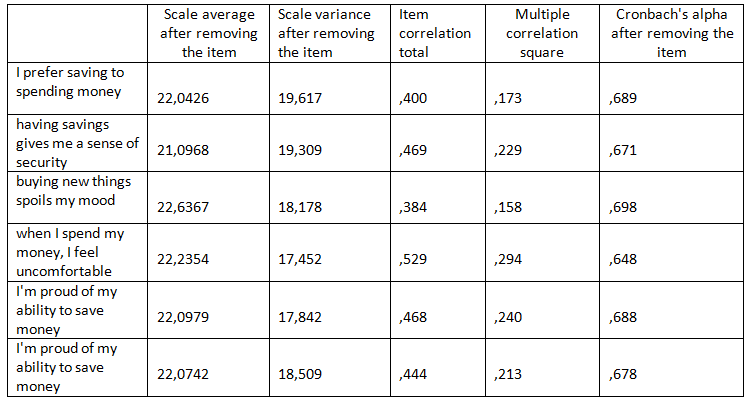
Tabelle 2 zeigt die Statistiken für die gesamte Skala, wenn wir eines der Items weglassen:
- Die erste Spalte gibt an, wie hoch der Durchschnitt der gesamten Skala wäre, wenn die Aussage aus der Skala entfernt würde. Dies wird berechnet, indem man den Mittelwert für das Item vom Mittelwert für die gesamte Skala abzieht. Natürlich führt eine Position, die aus der Skala entfernt wird, immer zu einem niedrigeren Durchschnitt, mehr noch, der Bereich der möglichen Werte ändert sich (eine Skala, die aus sechs Items besteht, kann Werte von 6 bis 36 haben, und eine Skala, die aus fünf Items besteht – von 5 bis 30);
- Wird ein Item aus der Skala entfernt, verringert sich auch die Varianz. Die Werte der Skalenvarianz nach dem Entfernen der einzelnen Items sind in der zweiten Spalte der Tabelle zu finden;
- Die dritte Spalte zeigt die Korrelation zwischen dem Skalen-Item und allen anderen Items zusammengenommen. Sie wird als Korrelationskoeffizient Pearson’s R zwischen dem Itemwert und der Summe der Werte der anderen Items berechnet. Wenn wir eine Skala erstellen, wollen wir in der Regel, dass die Korrelation zwischen den einzelnen Elementen und der gesamten Skala hoch ist. Andernfalls könnte der Verdacht aufkommen, dass das Item nicht genau dasselbe Konstrukt wie die anderen misst, und dies ist eine Voraussetzung dafür, dass das Item aus der Skala entfernt werden sollte. In unserem Beispiel ist der niedrigste Korrelationskoeffizient mit der gesamten Skala für das Item Neue Dinge kaufen verdirbt mir die Laune;
- Die vierte Spalte zeigt das multiple Korrelationsquadrat, das Sie wahrscheinlich von der Regressionsanalyse mit dem R-Quadrat kennen. Für jede Skalenposition wird ein Regressionsmodell erstellt, in dem das Item eine abhängige Variable ist und alle anderen Items die Rolle der Prädiktoren übernehmen. Ziel ist es, die Werte für diese Skalenposition auf der Grundlage der Kenntnis der Werte aller anderen Positionen vorherzusagen. Je höher das R-Quadrat, desto besser;
- Die letzte Spalte der Tabelle enthält Informationen über den Cronbachs Alpha-Wert nach Streichung des betreffenden Items. Wie wir bereits wissen, beträgt Cronbachs Alpha für die gesamte Skala 0,71. Wenn aus der Tabelle hervorgeht, dass die Streichung eines Items den Cronbachs Alpha-Wert verbessern (erhöhen) würde, wäre dies ein starkes Argument für uns, unsere Skala auf fünf Items zu reduzieren.
Auf der Grundlage früherer Analysen haben wir vermutet, dass die Aussage „Neue Dinge kaufen verdirbt mir die Laune“ die Konsistenz der Skala beeinträchtigen könnte. Schauen wir uns an, was passiert, wenn wir sie entfernen. Aus dieser Tabelle können wir ablesen, dass sich der Cronbachs Alpha-Wert nach dem Entfernen dieser Position verringern würde, auch wenn der Rückgang relativ gering wäre. Die Streichung jeder anderen Position würde zu einem stärkeren Rückgang führen. In diesem Fall ist die endgültige Entscheidung dem Analysten überlassen. Vielleicht würden einige von Ihnen es vorziehen, diese Variable zu belassen, um Cronbachs Alpha zu maximieren. Wenn wir jedoch wollen, dass unsere Skala nicht zu kompliziert ist (nach der Regel: je einfacher, desto besser), können wir beschließen, das Item zu entfernen, das nicht viel zu unserer Skala beiträgt.
Führen wir also die Reliabilitätsanalyse noch einmal durch, aber dieses Mal ohne diese Variable.
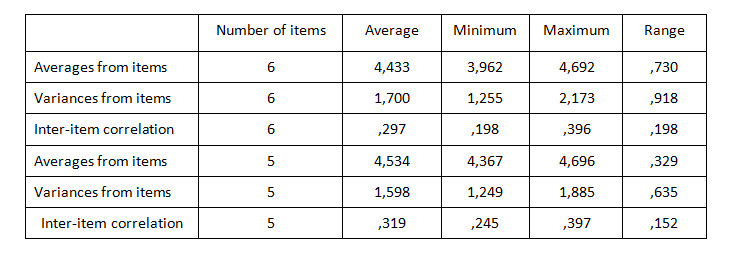
Table 3. Zusammenfassende Statistik der Items – vor und nach der Entfernung der Variable „Neue Dinge kaufen verdirbt meine Laune“.
Beachten Sie, dass wir darauf achten müssen, nicht zu übertreiben, damit die Skalenpunkte einander ähnlich werden. Stellen Sie sich vor, alle Skalenitems sind perfekt miteinander korreliert und haben die gleichen Mittelwerte und Varianzen. In einer solchen Situation stellt sich die Frage: Warum überhaupt eine Skala konstruieren? Anstatt den gesamten Satz von Variablen zu analysieren, würde es genügen, eine beliebige Variable aus dem Satz auszuwählen. Die Analyse dieser Variablen würde genau die gleichen Ergebnisse liefern wie die Analyse der gesamten Gruppe. Um sich jedoch nicht im Streben nach Exzellenz zu verzetteln, können wir statistische Tests verwenden, die im Rahmen des Verfahrens der Zuverlässigkeitsanalyse zur Verfügung stehen.
Ein Ansatz kann darin bestehen, zu versuchen, unsere Daten an ein paralleles oder eng paralleles Modell anzupassen. Das streng parallele Modell geht davon aus, dass in der Grundgesamtheit alle Skalenitems die gleichen Mittelwerte und Varianzen aufweisen. Im Falle des parallelen Modells ist die Nullhypothese nicht so restriktiv und geht nur von der Gleichheit der Varianz zwischen den Skalenitems aus. Beachten Sie, dass das parallele Modell im streng parallelen Modell verschachtelt ist: Wenn die Annahmen des parallelen Modells nicht erfüllt sind, dann ist automatisch ausgeschlossen, dass die Annahmen des streng parallelen Modells erfüllt sind.
Versuchen wir nun, das parallele Modell an unsere Daten anzupassen. Nachstehend finden Sie eine Tabelle mit dem Modellanpassungstest. Dieser Test prüft, ob die Daten die Annahme der Nullhypothese zulassen, dass es keine Unterschiede zwischen den Varianzen der einzelnen Skalenpositionen gibt.

Table 4. Paralleler Modellanpassungstest
Ein Signifikanzniveau des Tests von weniger als 0,05 bedeutet, dass es keinen Grund gibt, die Nullhypothese anzunehmen. Für uns bedeutet dies, dass sich die Varianz mindestens eines Items signifikant von der Varianz der anderen Items unterscheidet. Wenn dies der Fall ist, ist es nicht mehr notwendig, den Übereinstimmungstest für das streng parallele Modell durchzuführen.
Wir wissen bereits, dass die Items unserer Skala nicht die gleiche Varianz haben, aber was ist mit ihren Mittelwerten? Um dies zu überprüfen, können wir Tests auf der Grundlage der ANOVA-Tabelle verwenden. Mit diesen Tests können wir die Nullhypothese überprüfen, die besagt, dass die Mittelwerte aller Items in der Grundgesamtheit gleich sind. Die Auswahl des geeigneten Tests hängt von der Messstufe der Variablen ab. Der F-Test wird verwendet, wenn die Variablen der Skala auf einer quantitativen Ebene gemessen werden, der Friedman-Test wird zur Analyse von Ordinalvariablen verwendet, und der Cochran-Test sollte gewählt werden, wenn es sich bei der Skala um eine dichotome Menge handelt. Unsere Skala besteht aus Elementen, die auf ordinaler Ebene gemessen werden, daher wähle ich den Friedman-Test.
In Tabelle 5 können wir den Wert des Friedman-Chi-Quadrat-Tests ablesen. Dies ist das Verhältnis der Summe der Quadrate zwischen den Items (35.559) und dem durchschnittlichen Intra-Objekt-Quadrat (1.101).
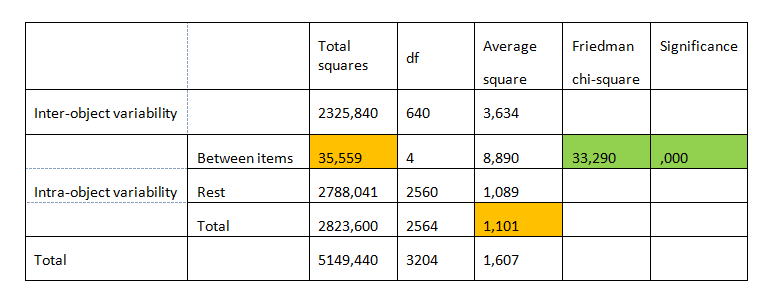
Table 5. ANOVA mit Friedman Test
Das Signifikanzniveau des Tests ist kleiner als 0,05. Folglich gibt es keine Grundlage für die Annahme der Nullhypothese. Dies bedeutet, dass der Durchschnitt mindestens eines Items signifikant von den anderen Durchschnittswerten abweicht.
Die statistischen Tests (sowohl der parallele Modellanpassungstest als auch der ANOVA-Tabellentest) haben uns versichert, dass die Skala zwar konsistent ist, wir aber nicht übertrieben haben, um diese Konsistenz zu erreichen. Es kann nicht behauptet werden, dass alle Items der Skala genau die gleichen Informationen enthalten. Die Verwendung nur einer ausgewählten Variablen anstelle der gesamten Skala würde dazu führen, dass alle zusätzlichen Informationen, die von den anderen Skalenpunkten geliefert werden, verloren gehen.
In diesem Beitrag haben wir nach Abwägung der Argumente dafür und dagegen beschlossen, eines der Items aus unserer Skala zu entfernen. Wir haben auch statistische Tests durchgeführt, um die Hypothesen über die Gleichheit der Mittelwerte und der Varianz zwischen den Items zu überprüfen. All dies zusammen hat es uns ermöglicht, zu erkennen, dass unsere Skala die Einstellung der Bankkunden zum Geldsparen gut widerspiegelt.
