by ANNA HUCULAK (Predictive Solutions)

Table 1. Reliability analysis result
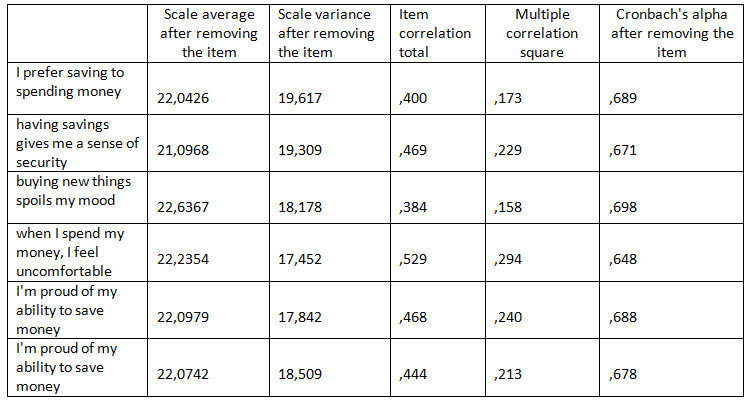
Table 2 shows the statistics for the whole scale when we omit one of the items:
- The first column tells us what the average of the whole scale would be if the statement was removed from the scale. This is calculated by subtracting the average for the item from the average for the whole scale. Of course, one position removed from the scale will always lead to a lower average, even more, the range of possible values will change (a scale consisting of six items can have values from 6 to 36, and a scale consisting of five items – from 5 to 30);
- One item removed from the scale will also reduce variance. The scale variance values after removing each of the items can be found in the second column of the table;
- The third column shows the correlation between the scale item and all the other items taken together. It is calculated as Pearson’s R correlation coefficient between the item value and the sum of values of the other items. Generally speaking, when we create a scale, we want the correlation between each element and the whole scale to be high. Otherwise, we may suspect that the item does not measure exactly the same construct as the others and this is a premise for considering the item to be removed from the scale. In our example, the lowest correlation coefficient with the whole scale is for the item buying new things spoils my mood;
- The fourth column shows the multiple correlation square, which you probably know from the R-square regression analysis. For each scale position, a regression model is built in which the item is a dependent variable and all other items assume the role of predictors. The aim is to predict the values for this scale item, based on knowledge of the values of all other items. The higher the R-square, the better;
- The last column of the table contains information about Cronbach’s alpha value after deleting the item concerned. As we know from earlier, Cronbach’s alpha for the whole scale is 0.71. If it would appear from the table that an item, if removed, would improve (increase) the Cronbach’s alpha value, it would be a strong argument for us to reduce our scale down to five items.
- On the basis of previous analyses, we suspected that the statement buying new things spoils my mood may adversely affect the consistency of the scale. Let’s see what happens if we remove it. We can read from this table that, after removing this item, Cronbach’s alpha value would be reduced, although the decrease would be relatively small. Removing any other position would result in a greater decline. In this case, the final decision is up to the analyst. Perhaps some of you would prefer to leave this variable to maximize Cronbach’s alpha. However, if we want our scale not to be too complicated (according to the rule: the simpler, the better), we can decide to remove the item that does not contribute much to our scale.
So let’s do the reliability analysis again, but this time with this variable omitted.
If we look at table 3, we can see that the correlations between the pairs of variables for the 5 items range from 0.245 to 0.397, and the average correlation increased to 0.319. There are also no such large differences between scale items in terms of averages or variances. It seems that it was a good idea to remove the item.
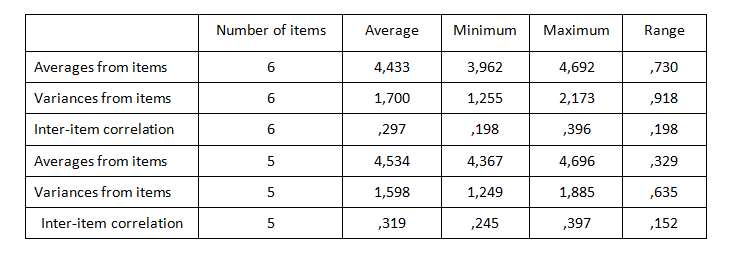
Table 3. Item summary statistics – before and after the removal of the variable “buying new things spoils my mood”

Table 4. Parallel model matching test
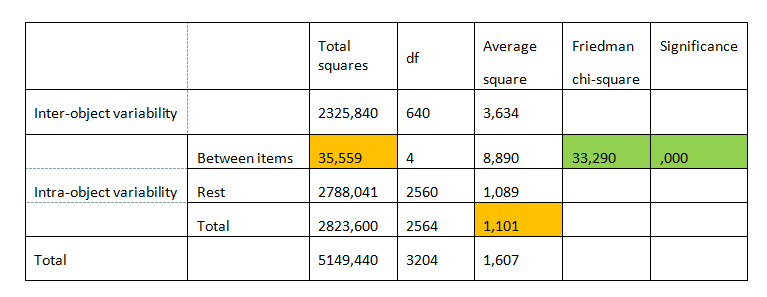
Table 5. ANOVA with Friedman test

