By RAFAŁ WAŚKO (Predictive Solutions)
The power of a test is the probability of detecting a statistically significant effect when one actually occurs in the population under study. Without adequate test power, we may make a type II error, meaning that the analyst will not reject the null hypothesis when it is in fact false. Calculating the power of a statistical test is often done prior to a study, which then allows a few key values to be determined to confirm the reliability of the results. Let’s analyse a situation in which a researcher uses a power of test analysis, or “power analysis”, to determine how large the research sample should be before starting the study. Testing too few people may result in failing to properly verify the hypotheses. The researcher will either not be able to see whether the lack of occurrence of the expected effect in the results is due to its actual absence in the study population, or because the study group was too small to observe it. A large sample, on the other hand, increases the cost of the study and increases the time to complete it. It is worth remembering that as the sample size increases, statistical tests become more capable of detecting small effects. The question here is whether the difference in results will be significant enough to incur additional costs, and prolong the study. Power analysis will determine the smallest sample size that will detect an effect for a given statistical test, at the level of significance desired by the researcher.WHAT DOES THE POWER OF A TEST DEPEND ON?
The power of a test will depend on three values: effect strength, sample size, and significance level. Effect strength is a quantitative representation of the magnitude of a phenomenon present in the population under study. Effect strength is calculated using a specific statistical measure, such as Pearson’s correlation coefficient for the relationship between quantitative variables, or Cohen’s d for the difference between groups. Let us look at one of the statistical tests. The Student’s t-test compares two groups to determine if there is a statistically significant difference between the results for the groups. The results of the test indicate that the groups are statistically significantly different. To determine how large the difference is, an additional measure is calculated, i.e., the strength of effect. In the case of t-tests, most often the strength of the effect is expressed by Cohen’s d statistic. It is worth mentioning that it is easier to empirically demonstrate the presence of strong effects than weak effects, because weak effects require statistical tests with greater power, a larger sample and more accurate measurement tools. Strong effects turn out to be statistically significant even with small samples, while weak effects require a larger sample to be significant. The sample size is the minimum number of units needed to observe an effect of a given size at a given level of test power. The significance level is the acceptable risk of making a type I error. The value of the statistical significance level is not arbitrarily imposed, but nevertheless 0.05 is often the accepted threshold for significance. The significance level is an important determinant of the power of a test and the magnitude of a type II error. Reducing the risk of a type I error automatically increases the risk of a type II error and reduces the power of the test.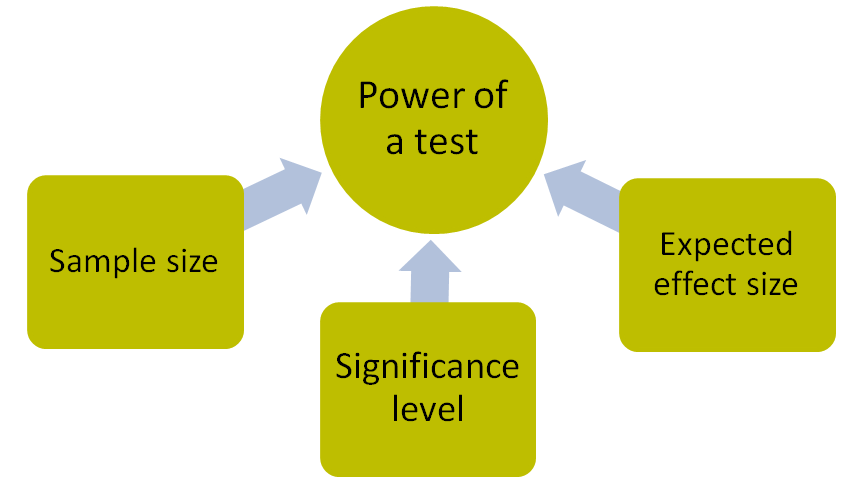
Figure 1. Constituent factors of test power
WHAT SHOULD BE THE MINIMUM POWER OF A STATISTICAL TEST?
Statistical hypothesis testing is associated with two errors whose probabilities we denote as α and β. As a reminder, the value of α is associated with making a type I error, i.e., mistakenly rejecting the null hypothesis when in fact it is true. The magnitude of β, on the other hand, is the probability of making a type II error, i.e., not rejecting a false null hypothesis. We can define the power of a test as the complement of the probability of making an error of the second kind (β), i.e., 1-β. It is generally accepted that the power of a test should be at least 0.8 to ensure that differences are detected and a type II error is avoided.
HOW TO INCREASE THE POWER OF THE TEST?
All four factors mentioned above are interrelated. We can increase the power of a test by:
- Increasing the size of the test sample.
- Increasing the significance level (in practice, however, the significance level is set at a value no greater than 0.05).
- Specifying that we will only be interested in significant effects.
HOW DO YOU CALCULATE THE POWER OF A STATISTICAL TEST?
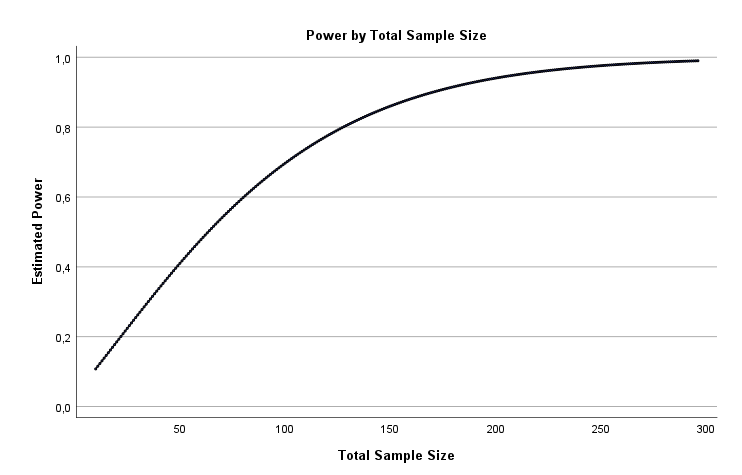
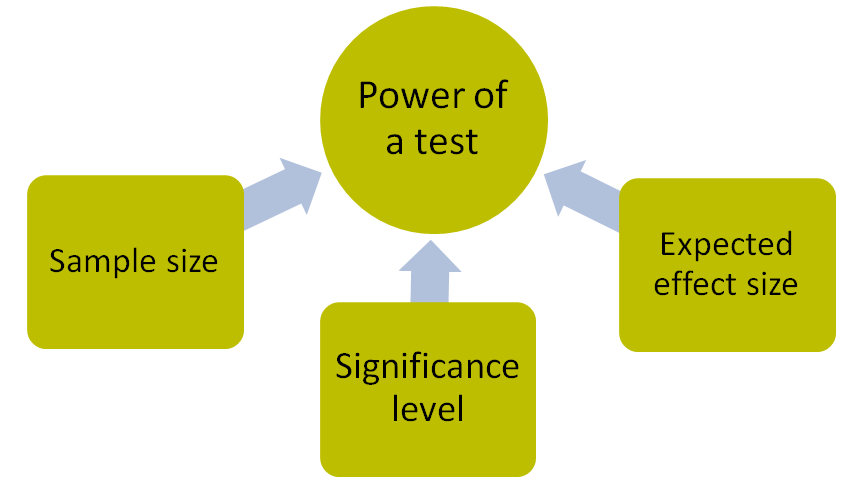
When analysing the power of a test, it is worth using a statistical programme to check which parameter values will be satisfactory in terms of the power of interest. Using PS IMAGO PRO, we can estimate the sample size on the basis of an indication of the test power and the effect strength of interest to the analyst. We can estimate what the sample size should be for a number of different test power values or within a certain range, e.g., from 0.5 to 0.9. The results obtained are presented in a table and on a graph. As can be seen in the table below, if we want to compare the results for two independent groups using a t-test, and assume that we are interested in an effect strength of 0.5 with a significance level of 0.05, then for the test power to be 0.8, there should be a minimum of 64 observations in each study group.