Von RAFAŁ WAŚKO (Predictive Solutions)

Bei der Datenanalyse ist es wichtig, ungewöhnliche Beobachtungen zu ermitteln, die sich deutlich von den anderen unterscheiden. Solche Werte, die als Ausreißer oder Ausreißerfälle bezeichnet werden, können die Ergebnisse der statistischen Analyse beeinträchtigen und zu falschen Schlussfolgerungen führen. In diesem Material werden wir uns ansehen, was Ausreißer sind, welche Arten von Ausreißern es gibt und wie solche Werte identifiziert werden können. Ausreißer sind in der statistischen Analyse wichtig. Sie können sich auf verschiedene Statistiken auswirken, z. B. auf den Mittelwert oder die Standardabweichung, was wiederum Auswirkungen auf statistische Tests, Korrelationsmessungen und die Modellierung von Daten haben kann und somit zu verzerrten Ergebnissen und Schlussfolgerungen führt. Daher ist die Identifizierung von Ausreißern und ihr angemessener Umgang mit ihnen durch Ersetzen, Entfernen oder den Einsatz geeigneter Techniken bei der Datenanalyse der Schlüssel zum Erhalt zuverlässiger und genauer statistischer Ergebnisse.

WAS SIND AUSREISSERFÄLLE?

Was wir als Ausreißer einstufen, hängt weitgehend von der Definition oder der gewählten Methode für die Suche nach Ausreißern ab. Eine allgemeine Definition von Ausreißern bedeutet, dass es sich um Werte handelt, die sich signifikant von anderen unterscheiden. Ausreißer können das Ergebnis von Messfehlern, einer schlecht ausgewählten Erhebungsstichprobe oder von Fehlern bei der Dateneingabe sein (z. B. manuelle Kodierung von Erhebungsergebnissen im Datensatz). Es ist auch erwähnenswert, dass Ausreißer nicht immer ein Zeichen für Fehler oder Unregelmäßigkeiten sind. Sie können auf seltene Ereignisse oder auf das Vorhandensein von Untergruppen von Daten mit unterschiedlichen Merkmalen zurückzuführen sein. In einigen Fällen sind Ausreißer wertvolle Informationen, die zur Identifizierung ungewöhnlicher Phänomene genutzt werden können. Bei der Datenanalyse ist es wichtig, den Kontext und den Zweck der Studie zu verstehen, um Ausreißer richtig interpretieren zu können. Im Folgenden finden Sie drei gängige Methoden zur Identifizierung von Ausreißern.

IDENTIFIZIERUNG VON AUSREISSERN IN EINDIMENSIONALEN DATEN

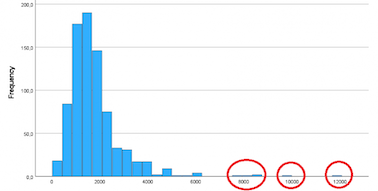
Es gibt viele Möglichkeiten, Ausreißer zu identifizieren. Die einfachste Methode, um festzustellen, ob es Ausreißer gibt, ist die Erstellung von Box-Plots oder Histogrammen. Genauere Methoden stützen sich auf geeignete statistische Maße, mit denen wir bestimmen können, welche Werte Ausreißer sind.

QUARTILSPANNE

Wir beginnen unsere Diskussion über Identifizierungsmethoden mit dem Quartilsbereich, aus dem Ausreißerbeobachtungen ermittelt werden können. Der Interquartilsbereich (IQR) ist die Differenz zwischen dem oberen (Q3) und dem unteren Quartil (Q1) der Daten[1]. Eine gängige Faustregel besagt, dass eine Beobachtung ein Ausreißer ist, wenn sie mindestens 1,5x über dem dritten Quartil oder 1,5x unter dem ersten Quartil liegt. Mit anderen Worten: Untere Ausreißer sind diejenigen, die unter Q1-1,5⋅IQR liegen, und obere Ausreißer sind diejenigen, die über Q3+1,5⋅IQR liegen.

Das obige Prinzip gilt auch für die Bestimmung der im Boxplot dargestellten Ausreißer, auf die weiter unten eingegangen wird.

STANDARDABWEICHUNG UND STANDARDISIERUNG

Die Standardabweichung misst, wie stark die Daten um den Mittelwert streuen. Werte, die unter Berücksichtigung der Standardabweichung erheblich vom Mittelwert abweichen, können als Ausreißer betrachtet werden. Eine einfache Möglichkeit, Ausreißer zu identifizieren, besteht darin, die Variable zu standardisieren. Dabei handelt es sich um eine Art Normalisierung einer Variablen, bei der vom Wert der Variablen ihr Mittelwert abgezogen wird und dieser Wert dann durch die Standardabweichung geteilt wird (Formel unten). Das Ergebnis ist eine neue Variable, bei der der Mittelwert 0 und die Standardabweichung 1 ist.

Die Formel für die Normierung für einen bestimmten Wert (x) lautet wie folgt:

wobei:

Z – standardisierter Wert

– Wert der Variablen

M – Mittelwert

– Standardabweichung

So können beispielsweise Werte, die um mehr als einen bestimmten Schwellenwert (z. B. das Zwei- oder Dreifache der Standardabweichung) vom Mittelwert entfernt sind, als Ausreißer betrachtet werden. Es sei auch daran erinnert, dass, wenn die Verteilung der analysierten Variablen eine Normalverteilung annimmt oder ihr nahe kommt, wir durch Anwendung der Drei-Sigma-Regel feststellen können, dass Beobachtungen, die innerhalb von 2 Standardabweichungen vom Mittelwert liegen, 95,4 % der Fälle sind, und im Falle von 3 Standardabweichungen vom Mittelwert sind es 99,7 % der Beobachtungen. Die Drei-Sigma-Regel kann bei der Identifizierung von Ausreißern hilfreich sein. Wenn wir davon ausgehen, dass die Beobachtungen um 3 Standardabweichungen vom Mittelwert abweichen, wissen wir, dass wir maximal 0,3 % der Beobachtungen der analysierten Variablen zurückweisen werden.

BOX PLOT UND HISTOGRAM

Ein Boxplot (oder Box-and-Whisker-Plot) ist ein visuelles Hilfsmittel, das die Verteilung von Daten und Ausreißerbeobachtungen zeigt. Werte, die außerhalb der Whisker (Linien, die sich von der Box aus erstrecken) liegen, können als Ausreißer betrachtet werden, d. h. sie enthalten diejenigen Beobachtungen, die innerhalb von 1,5 oder – 1,5 der Quartilspanne der Box liegen. Wie in der nachstehenden Box-Darstellung zu sehen ist, gibt es Punkte, die sowohl über dem oberen als auch über dem unteren Whisker liegen. Die kreisförmigen Punkte sind die Ausreißer, d. h. die Werte, die zwischen 1,5/-1,5 und 3/-3 der Quartilsspanne der Box liegen. Der sternförmige Punkt wird als Extremfall bezeichnet, und dies sind Beobachtungen, die mehr als 3/-3 Quartile von der Box entfernt sind.

Abbildung 1: Boxplot, der die Verteilung der Variablen Höhe (cm) zeigt.

Wie Sie sehen, haben wir mit einem Boxplot nicht nur die Möglichkeit, die Verteilung einer Variablen visuell darzustellen, sondern auch zu prüfen, ob es Ausreißer in den Daten gibt. Eine zweite Art der Visualisierung, die bei der Identifizierung von Ausreißern hilfreich sein kann, ist das Histogramm. Dieses Diagramm zeigt die Häufigkeitsverteilung der Daten in verschiedenen Wertintervallen (oder Klassen). Die Wertintervalle werden auf der horizontalen Achse dargestellt und die Anzahl des Auftretens der Daten in jedem Intervall wird auf der vertikalen Achse dargestellt. Werte, die sich deutlich abheben und an den extremen Enden des Histogramms liegen (am weitesten vom Rest der Daten entfernt), können als potenzielle Ausreißer betrachtet werden.

Abbildung 2: Histogramm, das die Verteilung der Variablen Nettomonatseinkommen zeigt. Die rote Farbe zeigt mögliche Ausreißer an.

IDENTIFIZIERUNG VON AUSREISSERN IN PS IMAGO PRO

Mit PS IMAGO PRO stehen mehrere Techniken zur Verfügung, die dem Analysten helfen können, Ausreißer zu identifizieren. Neben Boxplots und Histogrammen gibt es auch Validierungsverfahren und Data-Mining-Techniken. Ein lohnendes Verfahren, mit dem Sie anhand Ihrer eigenen Vorgaben schnell feststellen können, welche Beobachtungen als Ausreißer zu zählen sind, ist Data Audit.

Wenn Sie im Menü Predictive Solutions die Option Data Audit wählen, geben Sie an, welche quantitativen Variablen Sie analysieren möchten. In den Optionen können Sie dann unter Ausreißer die Statistiken angeben, anhand derer Ausreißer identifiziert werden sollen. Im Bereich Ausreißer können Sie zusätzlich festlegen, über/unter wie vielen Standardabweichungen vom Mittelwert oder über/unter wie vielen Quartilsintervallen ein bestimmter Wert als Ausreißer eingestuft wird.

Abbildung 3: Statistikauswahlfenster für quantitative Variablen im Datenauditverfahren

In diesem Beispiel verwende ich die Variable zur Anzahl der Jahre, die der Befragte in der Ausbildung verbracht hat. Dann wähle ich in den Optionen für quantitative Variablen im Bereich Ausreißer die Standardabweichung und die vierteljährliche Spanne aus. Die anderen Optionen lasse ich unverändert. Als Ergebnis erhalte ich eine Tabelle, die mir sagt, wie viele Beobachtungen nach den angegebenen Kriterien als Ausreißer gezählt werden.

Tabelle 1. Ergebnistabelle des Data-Audit-Verfahrens mit der Anzahl der identifizierten Ausreißer.

ZUSAMMENFASSUNG

Ausreißer sind ungewöhnliche Beobachtungen, die vom Rest der Daten abweichen. Es gibt viele Methoden zur Ermittlung von Ausreißern, z. B. Standardisierung, Interquartilsbereich, Box-Plots oder Histogramme. Die Interpretation von Ausreißern hängt vom Kontext und Zweck der Studie ab. Sie sind nicht immer etwas Schlechtes, können aber bei der Analyse der Daten von Bedeutung sein und die statistischen Ergebnisse und die daraus gezogenen Schlussfolgerungen beeinträchtigen. Es ist wichtig, bei der Datenanalyse auf potenzielle Ausreißer zu achten und zu beurteilen, ob sie behandelt werden müssen, damit die erzielten Ergebnisse genau und zuverlässig sind.

AUßREIßER ERKENNUNG. IDENTIFIKATION UND SIGNIFIKANZ IN DER DATENANALYSE