DIE DREI-SIGMA-REGEL

Von RAFAŁ WAŚKO (Predictive Solutions)

Die Drei-Sigma-Regel ist ein wichtiges Instrument in der Statistik und im Qualitätsmanagement. Im Rahmen der Datenanalyse ermöglicht sie die Identifizierung von Ausreißern, die sich signifikant vom Rest der Daten unterscheiden. Die Anwendung der Drei-Sigma-Regel in der Qualitätskontrolle deckt auch Anomalien auf und ermöglicht eine frühzeitige Erkennung von Problemen und eine wirksame Reaktion darauf, wodurch weitere Komplikationen vermieden werden können.

WAS IST SIGMA?

Zunächst ist es sinnvoll zu erklären, was „Sigma“ in der Statistik bedeutet. In der Statistik wird der griechische Buchstabe „σ“ (sigma) als Bezeichnung für die Standardabweichung verwendet. Sie ist ein Maß für die Streuung der Daten um den Mittelwert. Vereinfacht ausgedrückt, gibt sie an, wie stark die Werte einer Variablen vom Mittelwert abweichen. Je größer der Wert der Standardabweichung ist, desto größer ist die Variabilität der Daten.

In der Praxis ist die Standardabweichung ein äußerst wichtiges Maß, da sie es uns ermöglicht zu beurteilen, wie groß die Abweichung zwischen den einzelnen Beobachtungswerten und dem Mittelwert in der Regel ist. Auf diese Weise lässt sich feststellen, ob die Daten nahe am Mittelwert liegen (kleinere Standardabweichung) oder eine größere Streuung um den Mittelwert aufweisen (größere Standardabweichung).

ANNAHMEN DER DREI-SIGMA-REGEL

Bevor wir uns mit den Annahmen befassen, sollte kurz erklärt werden, was eine Normalverteilung ist. Die Geschichte der Drei-Sigma-Regel beginnt mit der Arbeit an der Normalverteilung. Diese Verteilung beschreibt die charakteristischen Eigenschaften vieler natürlicher Phänomene, wie physikalische Messungen, Testergebnisse und viele andere. Die Normalverteilung ist glockenförmig, und die meisten Daten gruppieren sich um einen Mittelwert, mit abnehmender Häufigkeit der Abweichung vom Mittelwert.

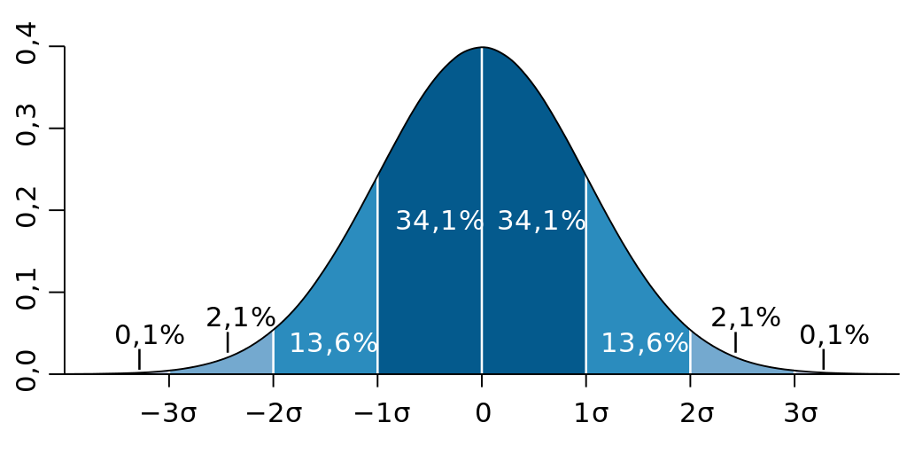
Die Drei-Sigma-Regel beruht auf der Annahme, dass eine Normalverteilung vorliegt:

Etwa 68,27 % der Beobachtungen liegen innerhalb einer Standardabweichung (σ) vom Mittelwert (μ).
Etwa 95,45 % der Beobachtungen liegen innerhalb von zwei Standardabweichungen vom Mittelwert.
Etwa 99,73 % der Beobachtungen liegen innerhalb von drei Standardabweichungen vom Mittelwert.

Abbildung 1.
Normalverteilung mit einzelnen Intervallen von einer Standardabweichung Breite
Quelle: https://en.wikipedia.org/wiki/Standard_deviation

Kurz gesagt, die Drei-Sigma-Regel besagt im Falle einer Normalverteilung, dass die überwiegende Mehrheit der Beobachtungen (99,73 %) zwischen drei Standardabweichungen unter dem Mittelwert und drei Standardabweichungen über dem Mittelwert liegt. Der Rest der Daten, der nur 0,27 % ausmacht, kann als Abweichung von der Norm betrachtet werden.

Es sei jedoch darauf hingewiesen, dass die Drei-Sigma-Regel auf der Annahme beruht, dass die Daten eine Normalverteilung aufweisen. In der Praxis können viele Phänomene unterschiedliche Verteilungen aufweisen, so dass der Anwendung dieser Regel eine Analyse der Verteilung der Daten und eine Bewertung vorausgehen sollte, ob diese Annahme erfüllt ist.

ANWENDUNG DER DREI-SIGMA-REGEL

Die in diesem Text vorgestellte Regel kann in einer Vielzahl von Bereichen angewendet werden, z. B. in der Fertigung, im Finanzwesen, in der Medizin oder in den Sozialwissenschaften. Bei der Qualitätskontrolle in der Fertigung kann sie häufig zur Überwachung von Produktionsprozessen und zur Ermittlung möglicher Probleme oder Abweichungen von der Norm verwendet werden. Wenn die Daten mehr als drei Sigma vom Mittelwert abweichen, kann dies auf Probleme im Produktionsprozess hinweisen. Ein zweites, beispielhaftes Anwendungsgebiet ist der medizinische Bereich. Bei der Analyse medizinischer Daten kann die Drei-Sigma-Regel helfen, Fälle oder Patientenergebnisse zu identifizieren, die vom Durchschnitt abweichen und möglicherweise besondere Aufmerksamkeit erfordern. Ein weiterer Bereich könnte die Sozialforschung sein, wo die Drei-Sigma-Regel dazu verwendet werden kann, abweichendes Verhalten oder Ereignisse zu identifizieren, die eine weitere Analyse erfordern.

ANWENDUNG DER DREI-SIGMA-REGEL IN DER QUALITÄTSKONTROLLE UND IN REGELKARTEN

Anfang des 20. Jahrhunderts begann Walter A. Shewhart, einer der Pioniere auf dem Gebiet der Produktionsmanagementprozesse, statistische Methoden zur Qualitätskontrolle in Produktionsprozessen einzusetzen. W. A. Shewhart war einer der Begründer der Regelkarten, die es ermöglichen, Produktionsprozesse zu überwachen und Abweichungen von der Norm zu erkennen.

Eine der wichtigsten Leistungen von W. A. Shewhart war die Anwendung der Drei-Sigma-Regel in der Qualitätskontrolle. Er führte das Konzept der Kontrollgrenzen ein, die ein Vielfaches der Standardabweichung waren und dazu dienten, festzustellen, wann ein Prozess Unregelmäßigkeiten aufwies. In Regelkarten wird die Drei-Sigma-Regel verwendet, um die Stabilität eines Prozesses zu überwachen und ihn innerhalb einer akzeptablen Variabilität zu halten. Die auf dieser Regel basierenden Kontrollgrenzen legen den Bereich fest, in dem sich der Prozess bewegen sollte. Punkte außerhalb der Drei-Sigma-Grenzen können auf mögliche Abweichungen von der Norm hinweisen, die weitere Analysen oder Korrekturmaßnahmen erfordern.

Die Analyse von Regelkarten nach der Drei-Sigma-Regel kann wie folgt erfolgen:

Innerhalb von 1σ: Wenn die meisten Punkte innerhalb von +/-1σ vom Mittelwert liegen, ist der Prozess stabil und kontrolliert,
Zwischen 1σ und 2σ: Wenn einige Punkte zwischen +/-1σ und +/-2σ liegen, kann der Prozess immer noch kontrolliert werden, aber die Variabilität kann etwas höher sein,
Zwischen 2σ und 3σ: Wenn die Punkte zwischen +/-2σ und +/-3σ liegen, kann das Verfahren eine gewisse Analyse erfordern, kann aber akzeptabel sein,
Über 3σ: Wenn die Punkte über +/-3σ hinausgehen, kann dies auf eine schwerwiegende Abweichung von der Norm und auf die Notwendigkeit von Korrekturmaßnahmen im Prozess hinweisen.

Abbildung 2.
Ein Beispiel für eine in PS IMAGO PRO erstellte Regelkarte. UCL und LCL sind Werte
die den empirischen 3-Sigma-Bereich über und unter dem durchschnittlichen Messwert abgrenzen

Ein wesentliches Merkmal der Drei-Sigma-Regel ist ihre Fähigkeit, Abweichungen von der Norm schnell zu erkennen und einzugreifen, um den Prozess wieder in einen kontrollierten Rahmen zu bringen. Durch das Erkennen von Problemen und das Ergreifen von Korrekturmaßnahmen ist es möglich, die Qualität von Prozessen und Produkten zu erhalten. Auf diese Weise unterstützt das Instrument die Unternehmen bei der Überwachung, der Verbesserung der Qualität und dem effektiven Qualitätsmanagement in verschiedenen Betriebsbereichen.

ZUSAMMENFASSUNG

Die Geschichte und Entstehung der Drei-Sigma-Regel geht auf die Arbeit an der Normalverteilung und der Qualitätskontrolle zurück. Diese Annahmen haben sich mit dem Fortschritt der Statistik weiterentwickelt und sind zu einem integralen Instrument der Datenanalyse, der Qualitätskontrolle und der Verbesserung von Fertigungsprozessen geworden. Mit der Drei-Sigma-Regel ist es möglich, Abweichungen von der Norm schnell zu erkennen und Korrekturmaßnahmen zu ergreifen, um die Einhaltung der Qualitätsanforderungen zu gewährleisten.

Abschließend sei darauf hingewiesen, dass die Drei-Sigma-Regel trotz ihrer Wirksamkeit bei der Erkennung von Abweichungen von der Norm bestimmte Einschränkungen aufweist, die bei ihrer Anwendung berücksichtigt werden müssen. Eine der wichtigsten ist die Erfüllung der Annahme der Normalverteilung. In der Praxis können die Daten unterschiedliche Verteilungen aufweisen, was die Wirksamkeit der Regel beeinträchtigen kann. Daher ist es wichtig, zu überprüfen, ob die Daten diese Annahme tatsächlich erfüllen. Es ist auch zu bedenken, dass die Drei-Sigma-Regel Abweichungen außerhalb der Drei-Sigma-Grenzen als potenzielle Probleme identifiziert. Allerdings sind nicht alle Abweichungen außerhalb dieses Bereichs gleichermaßen signifikant. Ein Punkt knapp außerhalb der Drei-Sigma-Grenze wird genauso behandelt wie ein Punkt, der viel weiter entfernt ist. Diese Einschränkung kann zu einer Überreaktion auf zufällige Veränderungen führen. Es ist wichtig, den Kontext zu verstehen, die Daten sorgfältig zu analysieren und die Annahmen zu überprüfen, um dieses Instrument in der Praxis wirksam einsetzen zu können.