DIE MESSNIVEAUS VON VARIABLEN

Von NATALIA GOLONKA (Predictive Solutions)

Das Messniveau ist eine der wichtigsten Eigenschaften von Variablen. Sie bestimmt, welche statistischen Tests dem Forscher im Laufe der Analyse zur Verfügung stehen. Aber welche Informationen vermittelt sie uns konkret? Ein Messniveau ist ein Messmuster, das es ermöglicht, den Grad oder die Menge einer Variablen zu identifizieren und zu bewerten. Diese Muster, die auch als Messskalen bezeichnet werden, ermöglichen eine klare und konkrete Darstellung von Variablen.

MESSSKALEN

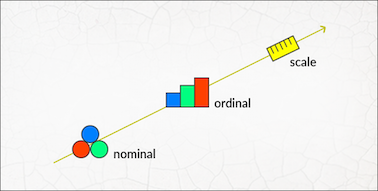
Es gibt vier grundlegende Messebenen:

1. Nominalskala
Hierbei handelt es sich um die unterste Ebene der Messung, bei der eine Analyseeinheit einer bestimmten Kategorie von Variablen zugeordnet wird. Die Kategorisierung muss zwei Bedingungen erfüllen: Sie muss erschöpfend sein und sich gegenseitig ausschließen. Folglich muss jede Beobachtung einer einzigen Kategorie zugeordnet werden, die auf sie zutrifft. Beispiele hierfür sind Geschlecht, Hautfarbe oder Geburtsland. Es gibt jedoch keine Reihenfolge oder Hierarchie innerhalb der Zuordnungen zu den Gruppen. Symbolisch ordnen wir ihnen oft fortlaufende Nummern zu, z. B. Geschlecht (1 – weiblich, 2 – männlich), aber das berechtigt uns nicht, algebraische Operationen mit ihnen durchzuführen.

Ein Sonderfall der nominalen Ebene der Messung ist die dichotome Variable, d. h. mit Null-Eins kodierte Variablen, z. B. Prüfungserfolg (bestanden/nicht bestanden). Auch Multiple-Choice-Fragen können dichotom kodiert werden, wobei jede mögliche Antwort eine eigene Variable darstellt. Obwohl wir theoretisch sagen können, dass z. B. die Kategorie „bestanden“ besser ist als „nicht bestanden“, können wir in der Praxis dichotome Variablen nicht im Rahmen einer Hierarchie berücksichtigen.

2. Ordinalskala
Auf dieser Ebene der Messung können die Daten nach einer bestimmten Hierarchie geordnet werden. Dabei wird davon ausgegangen, dass die Intensität einer Variablen ein Kontinuum ist, auf dem die verschiedenen Kategorien der Variablen geordnet werden können. Ein solches Beispiel wäre der Schwierigkeitsgrad der Aufgabe (leicht, mittel, schwer) oder das Bildungsniveau (von der frühen Kindheit bis zur Hochschulbildung). In diesem Fall ist es jedoch notwendig, sich über die Art der Daten zu vergewissern; wenn sich herausstellt, dass die Kategorien bestimmte Schultypen umfassen (allgemeinbildende Schulen, technische Schulen, Berufsschulen), dann wird diese Variable auf einer Nominalskala gemessen, da es nicht möglich ist, den Kategorien eine logische Reihenfolge zuzuweisen.

Die Ordinalskala ermöglicht die Angabe der Intensität des untersuchten Phänomens, d. h., dass eine bestimmte Beobachtung größer, älter, ressourcenintensiver usw. ist. Für die Analyse selbst spielt es keine Rolle, ob die Reihenfolge aufsteigend oder absteigend ist. Wichtig ist, dass es eine logische Abfolge von Kategorien gibt.

Die Likert-Skala ist ein weiteres Beispiel für eine ordinale Ebene der Messung. Sie wird häufig in der Psychologie und Soziologie verwendet und zeichnet sich dadurch aus, dass der Befragte seine Einstellung zu einer bestimmten Aussage auf einer Skala von normalerweise 1-5 oder 1-7 angibt. Zum Beispiel:

Erklärung: Die Produkte von Unternehmen X sind innovativ.

Antwort:

1. Stimme voll und ganz zu
2. Stimme zu
3. Habe keine Meinung
4. Stimme nicht zu
5. Stimme überhaupt nicht zu

Wenn wir die Ergebnisse später als Gruppe analysieren, können wir also eine Antwort auf die Frage erhalten, welche Produkte eines Unternehmens als innovativer angesehen werden. Allerdings lässt sich daraus nicht ableiten, wie groß der Unterschied bei dieser Innovation ist.

3.Intervall-Skala
Mit der Intervallskala können wir Daten miteinander vergleichen und die Differenz zwischen ihnen bestimmen, d. h. ihren Abstand zueinander auf der verwendeten Skala messen. Die numerischen Werte der einzelnen Variablen sind also nicht mehr nur symbolisch. Auf der Intervallebene der Messung gibt es jedoch immer noch keinen absoluten Nullpunkt. Ein gutes Beispiel dafür ist die Messung der Temperatur auf der Celsius-Skala: Wenn gestern 10 °C herrschten und heute 10 °C mehr, wissen wir ohne großen Aufwand, dass heute 20 °C herrschen. Aber können wir sagen, dass es doppelt so warm ist? Wahrscheinlich können wir es erahnen, aber was ist, wenn die Ausgangstemperatur -5 °C beträgt?

Mit der Intervallskala lässt sich also feststellen, um wie viel sich die einzelnen Werte unterscheiden.

4. Verhältnis-Skala
Dies ist die genaueste Messstufe. Denn mit der Verhältnisskala kann man (wie der Name schon sagt) bestimmen, um wie viel Prozent sich die verschiedenen Werte voneinander unterscheiden. Um auf das vorherige Beispiel zurückzukommen: Um die Temperatur auf einer relativen Skala zu messen, muss die Kelvin-Skala verwendet werden. Sie wird als absolute Skala bezeichnet, weil sie einen absoluten Nullpunkt enthält. Obwohl es sich dabei nur um eine theoretische Annahme handelt (laut Physik ist dies der Zustand des Stillstands aller Schwingungen der Moleküle, der in der Praxis nicht erreicht werden kann), können die auf dieser Skala ausgedrückten Temperaturen bereits frei miteinander verglichen werden, z. B. sind 20 K doppelt so viel wie 10 K.

Ein weiteres Beispiel ist das Alter eines Autos. Wird es als Jahrgang des Fahrzeugs angegeben (z. B. 2019, 2023 usw.), dann wird diese Variable auf einer Intervallskala gemessen; wir können den Unterschied im Alter der Autos bestimmen, weil die Null auf dieser Skala nur konventionell ist (sie beginnt „unsere Ära“). Wenn wir uns jedoch dafür entscheiden, diese Information in Jahren darzustellen, können wir davon ausgehen, dass ein Auto, das gerade vom Band läuft, 0 Jahre alt ist, während ein im Jahr 2019 hergestelltes Auto heute 4 Jahre alt sein wird.

QUALITATIVE UND QUANTITATIVE VARIABLEN

An dieser Stelle sollte kurz auf die Unterteilung der Variablen in qualitative und quantitative Variablen hingewiesen werden. Zu den qualitativen Variablen gehören Variablen, die auf nominalen und ordinalen Skalen gemessen werden. Sie haben spezifische Kategorien, deren Aufteilung erschöpfend ist und die sich gegenseitig ausschließen (wie bereits erwähnt). Quantitative Variablen hingegen haben Eigenschaften, die wir genau messen können. Die Skalen, die dies ermöglichen, sind die Intervall- und Verhältnisebenen der Messung. Bei der Arbeit in PS IMAGO PRO werden diese beiden Arten von Messskalen als eine einzige Messstufengruppe behandelt. Der Analytiker hat also die Wahl zwischen drei Skalen: nominal, ordinal und quantitativ. Es ist wichtig, dass jeder Variablen das richtige Messniveau zugewiesen wird, da dies für die nachfolgenden Analysen entscheidend ist. Jeder statistische Test hat seine Grenzen, und es ist nicht ungewöhnlich, dass diese Grenzen genau mit der Art und Weise zusammenhängen, in der die Variablen gemessen werden.

DISKRETE UND KONTINUIERLICHE VARIABLEN

Eine weitere Unterteilung, die sich auf die Ebene der Messung bezieht, ist die Unterscheidung zwischen diskreten und kontinuierlichen Variablen. Diskrete Variablen sind jene Variablen, die eine endliche Anzahl von Werten annehmen. Diese Werte können ganzzahligen natürlichen Zahlen zugeordnet werden, wobei zwischen zwei „benachbarten“ diskreten Werten keine anderen Werte gefunden werden können. In der Praxis handelt es sich bei solchen Variablen in der Regel um solche, die auf einer nominalen oder ordinalen Skala gemessen werden, z. B. bei der Augenfarbe (1 – braun, 2 – blau, 3 – andere) kann man einer Beobachtung logischerweise keinen Wert von z. B. 2,5 zuordnen. Es gibt jedoch auch quantitative Variablen, die als diskret eingestuft werden können. Beispiele hierfür sind die Anzahl der Kinder in einer Familie, die Passagiere auf einem Schiff oder die Ergebnisse eines Tests mit Ja/Nein-Fragen. Aufgrund der Natur solcher Variablen ist die Menge ihrer Werte endlich und es ist nicht möglich, eine nicht ganzzahlige Zahl logisch zu begründen. Kontinuierliche Variablen hingegen können beliebige Werte annehmen, manchmal innerhalb eines begrenzten (hauptsächlich durch die Naturgesetze bedingten) Bereichs, z. B. wenn wir die Größe von Menschen oder die Temperatur der Umgebung untersuchen. Zwischen zwei Werten können wir jedoch unendlich viele andere Werte beobachten. Die einzige Einschränkung ist hier die Genauigkeit der uns zur Verfügung stehenden Messung.

MESSEBENEN UND STATISTIKEN

Wie bereits erwähnt, kann das Messniveau eine gewisse Einschränkung bei der Auswahl der zu berechnenden Statistiken darstellen. Betrachten wir nun eine der grundlegendsten deskriptiven Statistiken, die zentrale Tendenz. Wie Sie sich vielleicht denken können, hat die Nominalskala die meisten Einschränkungen. Wir können den Modus berechnen, aber der Mittelwert oder der Median ist nicht verfügbar. Um auf das Beispiel mit der Augenfarbe zurückzukommen, können wir sagen, welcher Wert am häufigsten beobachtet wurde (dominant/modal), aber da die Kategorien nicht geordnet sind, kann weder die Mitte des Bereichs (Median) noch der „durchschnittliche“ Wert (Mittelwert) der Augenfarbe berechnet werden. Wenn die Variable auf einer Ordinalskala gemessen wird, kann zusätzlich zum Modus auch der Median berechnet werden, z. B. bei der Analyse einer Variablen, die sich auf den aktuellen Bildungsstand der Befragten bezieht, kann die dominante Kategorie die Grundschulstufe sein (die längste Schulzeit und daher die meisten Kinder), der Median wird jedoch die Kategorie der Sekundarschulstufe sein. Wir können also sowohl Informationen über die vorherrschende Kategorie (in Bezug auf die Anzahl) erhalten als auch darüber, welche Kategorie in unserer Stichprobengruppe in der Mitte des Spektrums liegt. Der Mittelwert bleibt für uns unzugänglich. Quantitative Skalen ermöglichen die Berechnung aller drei Statistiken. Die oben genannten Informationen sind in Tabelle 1 zusammengefasst.

Tabelle 1. Verfügbarkeit von ausgewählten Statistiken für jede Ebene der Messung.

Die begrenzte Fähigkeit, Statistiken zu berechnen, schlägt sich auch in der Verfügbarkeit statistischer Tests nieder. Wenn wir die theoretische Grundlage der verschiedenen Methoden der Datenanalyse kennen, wissen wir, ob sie auf den uns vorliegenden Datensatz angewendet werden können. Wenn wir z. B. wissen, dass die Varianzanalyse auf gruppenübergreifenden Mittelwerten beruht, wissen wir auch, dass die abhängigen Variablen, die wir für einen solchen Test verwenden wollen, auf einer quantitativen Skala gemessen werden müssen.

Natürlich gibt es auch statistische Tests zur Analyse von qualitativen Variablen. Ein Beispiel hierfür ist der Chi-Quadrat-Test[1], bei dem die zugrundeliegende Statistik die Anzahl in den einzelnen Gruppen ist.

ZUSAMMENFASSUNG

Das Messniveau ist eine wichtige Eigenschaft jeder Variablen, und seine korrekte Zuordnung zu jeder Variablen in der Phase der Datenerstellung ist entscheidend, wenn die weiteren Analysen zuverlässig und relevant sein sollen.

Obwohl die Vertrautheit mit statistischen Tests und ihren theoretischen Grundlagen die Arbeit des Analytikers erheblich erleichtert, können auch die von der Statistiksoftware bereitgestellten Hinweise nützlich sein: Bei der Auswahl von Variablen für die Analyse in PS IMAGO PRO wird die Software Informationen darüber liefern, dass ein bestimmtes Messniveau in dem jeweiligen Verfahren nicht verwendet werden kann. Bei der Arbeit mit Daten können wir auch Transformationen durchführen, die unsere Daten in bestimmte Gruppen unterteilen, z. B. können wir für die Zwecke einer gewünschten statistischen Analyse das in Jahren ausgedrückte Alter (quantitative Skala) in eine bestimmte Anzahl von Altersgruppen (Ordinalskala, z. B. 18-30, 31-50 und 51+) umwandeln. In besonderen Fällen können wir eine neue Ordinalvariable auf der Grundlage einer Nominalvariable erstellen. Ein Beispiel dafür wäre, die Namen der von den Befragten besuchten Schulen in Kategorien von Bildungsstufen umzuwandeln, z. B. die Fachschule für Gastronomie in die Gruppe der Sekundarstufe, alle Grundschulen in die Kategorie der Primarstufe usw. In der Regel ist es jedoch einfacher, von den präziseren Ebenen der Messung zu den einfacheren zu wechseln. Dies gibt dem Analysten zwar eine gewisse Flexibilität, aber das Verständnis des Problems der Messung einer Variablen schützt den Forscher vor Fehlern, wie z. B. der Berechnung des Durchschnitts einer Provinz oder eines Studienfachs, und erleichtert die Auswahl von Analysen im Kontext der vorliegenden Daten.

[1] https://ps-imago-pro.2×4.de/en/pearsons-chi-square-test-of-independence/