DIE STÄRKE (POWER) EINES STATISTISCHEN TESTS

Von RAFAŁ WAŚKO (Predictive Solutions)

Die Stärke eines Tests ist die Wahrscheinlichkeit, einen statistisch signifikanten Effekt festzustellen, wenn dieser in der untersuchten Population tatsächlich eintritt. Ohne eine angemessene Teststärke kann es zu einem Fehler vom Typ II kommen, was bedeutet, dass der Analytiker die Nullhypothese nicht zurückweist, obwohl sie in Wirklichkeit falsch ist. Die Berechnung der Aussagekraft eines statistischen Tests wird häufig vor Beginn einer Studie durchgeführt, wodurch einige Schlüsselwerte zur Bestätigung der Zuverlässigkeit der Ergebnisse ermittelt werden können. Analysieren wir eine Situation, in der ein Forscher eine Teststärkeanalyse oder „Power-Analyse“ verwendet, um zu bestimmen, wie groß die Forschungsstichprobe vor Beginn der Studie sein sollte. Wenn zu wenige Personen getestet werden, kann dies dazu führen, dass die Hypothesen nicht richtig überprüft werden können. Der Forscher wird entweder nicht in der Lage sein zu erkennen, ob das Ausbleiben des erwarteten Effekts in den Ergebnissen auf sein tatsächliches Fehlen in der Studienpopulation zurückzuführen ist oder darauf, dass die Studiengruppe zu klein war, um ihn zu beobachten. Eine große Stichprobe hingegen erhöht die Kosten der Studie und verlängert die Zeit für ihre Durchführung. Es ist zu bedenken, dass statistische Tests mit zunehmender Stichprobengröße immer besser in der Lage sind, kleine Effekte zu erkennen. Hier stellt sich die Frage, ob der Unterschied in den Ergebnissen signifikant genug sein wird, um zusätzliche Kosten zu verursachen und die Studie zu verlängern. Mit der Power-Analyse wird die kleinste Stichprobengröße ermittelt, mit der ein Effekt für einen bestimmten statistischen Test auf dem vom Forscher gewünschten Signifikanzniveau nachgewiesen werden kann.

WOVON HÄNGT DIE AUSSAGEKRAFT EINES TESTS AB?

Die Aussagekraft eines Tests hängt von drei Werten ab: Effektstärke, Stichprobengröße und Signifikanzniveau. Die Effektstärke ist eine quantitative Darstellung des Ausmaßes eines in der untersuchten Population vorhandenen Phänomens. Die Effektstärke wird anhand eines bestimmten statistischen Maßes berechnet, z. B. des Korrelationskoeffizienten von Pearson für die Beziehung zwischen quantitativen Variablen oder von Cohen’s d für den Unterschied zwischen Gruppen. Schauen wir uns einen der statistischen Tests an. Der Student’s t-Test vergleicht zwei Gruppen, um festzustellen, ob es einen statistisch signifikanten Unterschied zwischen den Ergebnissen der Gruppen gibt. Die Ergebnisse des Tests zeigen, dass sich die Gruppen statistisch signifikant unterscheiden. Um festzustellen, wie groß der Unterschied ist, wird ein zusätzliches Maß berechnet, nämlich die Stärke des Effekts. Bei t-Tests wird die Stärke des Effekts meist durch Cohens d-Statistik ausgedrückt. Es ist erwähnenswert, dass es einfacher ist, das Vorhandensein starker Effekte empirisch nachzuweisen als schwache Effekte, da schwache Effekte statistische Tests mit größerer Aussagekraft, eine größere Stichprobe und genauere Messinstrumente erfordern. Starke Effekte erweisen sich auch bei kleinen Stichproben als statistisch signifikant, während schwache Effekte eine größere Stichprobe erfordern, um signifikant zu sein. Der Stichprobenumfang ist die Mindestanzahl von Einheiten, die erforderlich ist, um einen Effekt einer bestimmten Größe bei einer bestimmten Teststärke zu beobachten. Das Signifikanzniveau ist das akzeptable Risiko, einen Fehler vom Typ I zu machen. Der Wert des statistischen Signifikanzniveaus ist nicht willkürlich festgelegt, aber dennoch ist 0,05 häufig die akzeptierte Schwelle für Signifikanz. Das Signifikanzniveau ist eine wichtige Determinante für die Aussagekraft eines Tests und das Ausmaß eines Fehlers vom Typ II. Eine Verringerung des Risikos eines Fehlers vom Typ I erhöht automatisch das Risiko eines Fehlers vom Typ II und verringert die Aussagekraft des Tests.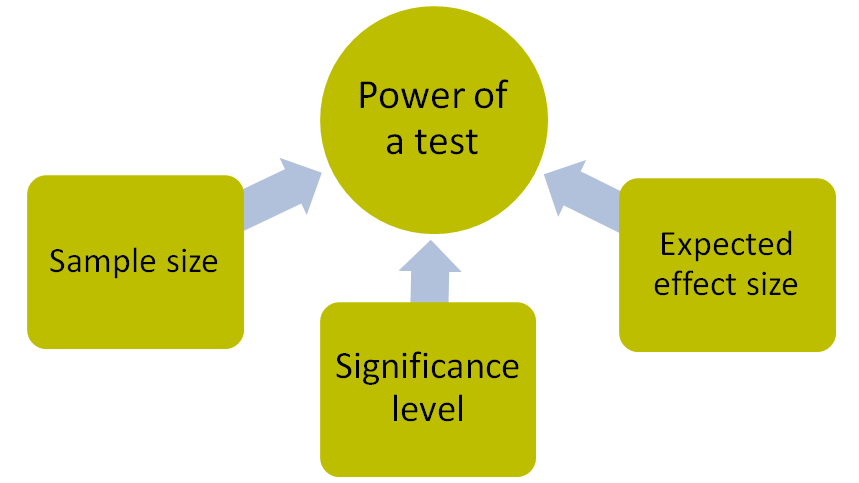

Abbildung 1. Faktoren, aus denen sich die Test Power zusammensetzt

An dieser Stelle ist auch zu erwähnen, dass sich statistische Tests in ihrer Aussagekraft unterscheiden. Parametrische Tests haben im Allgemeinen eine höhere Aussagekraft als nicht-parametrische Tests. Eine weitere Überlegung betrifft die Größe der Teststichprobe und die Größe des erwarteten Effekts. Je größer die Stichprobe ist, desto größer ist die Aussagekraft des Tests. Es ist zu bedenken, dass Fehler auf der Ebene der Studiendurchführung ebenfalls die Aussagekraft des Tests beeinträchtigen und dazu führen, dass das Ergebnis mit Fehlern behaftet ist.

WIE HOCH SOLLTE DIE MINDESTSTÄRKE EINES STATISTISCHEN TESTS SEIN?

Die statistische Hypothesenprüfung ist mit zwei Fehlern verbunden, deren Wahrscheinlichkeiten wir mit α und β bezeichnen. Zur Erinnerung: Der Wert von α ist mit einem Fehler vom Typ I verbunden, d. h. mit der irrtümlichen Ablehnung der Nullhypothese, obwohl diese in Wirklichkeit wahr ist. Die Größe von β hingegen ist die Wahrscheinlichkeit, einen Fehler vom Typ II zu machen, d. h. eine falsche Nullhypothese nicht zurückzuweisen. Wir können die Aussagekraft eines Tests als das Komplement der Wahrscheinlichkeit eines Fehlers zweiter Art (β), d.h. 1-β, definieren. Es ist allgemein anerkannt, dass die Aussagekraft eines Tests mindestens 0,8 betragen sollte, um sicherzustellen, dass Unterschiede erkannt werden und ein Fehler vom Typ II vermieden wird.

WIE LÄSST SICH DIE AUSSAGEKRAFT DES TESTS ERHÖHEN?

Alle vier oben genannten Faktoren sind miteinander verknüpft. Wir können die Aussagekraft eines Tests erhöhen, indem wir:

den Umfang der Testprobe erhöhen
das Signifikanzniveaus anheben (in der Praxis wird das Signifikanzniveau jedoch auf einen Wert von höchstens 0,05 festgelegt).
angeben, dass wir nur an signifikanten Auswirkungen interessiert sind.

WIE BERECHNET MAN DIE AUSSAGEKRAFT EINES STATISTISCHEN TESTS?

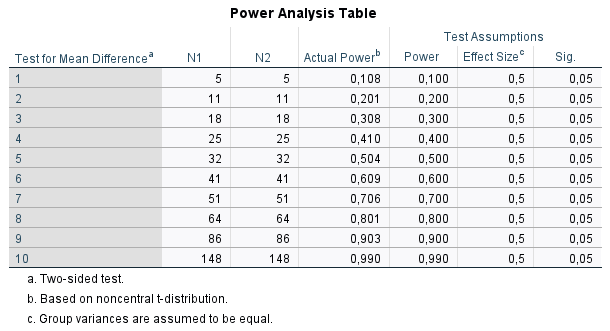
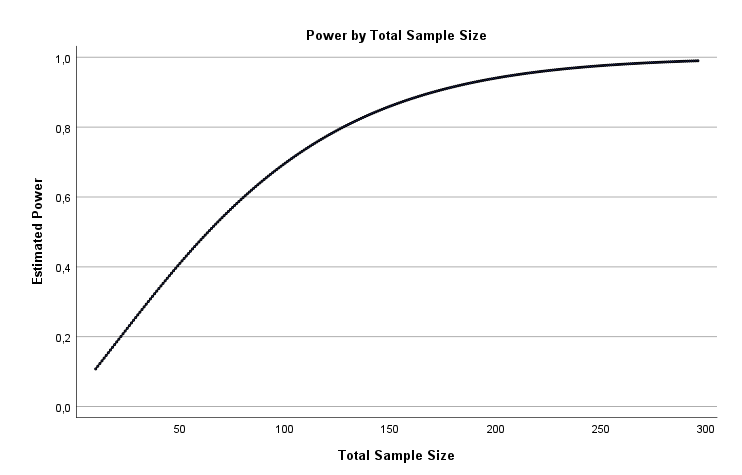
Bei der Analyse der Aussagekraft eines Tests lohnt es sich, mit einem Statistikprogramm zu prüfen, welche Parameterwerte für die gewünschte Aussagekraft ausreichen. Mit PS IMAGO PRO können wir den Stichprobenumfang auf der Grundlage einer Angabe der Teststärke und der Effektstärke, die für den Analysten von Interesse ist, schätzen. Es kann geschätzt werden, wie groß die Stichprobe für verschiedene Werte der Teststärke oder innerhalb eines bestimmten Bereichs, z. B. von 0,5 bis 0,9, sein sollte. Die Ergebnisse werden in einer Tabelle und in einem Diagramm dargestellt. Wie in der nachstehenden Tabelle zu sehen ist, sollten, wenn wir die Ergebnisse für zwei unabhängige Gruppen mit einem t-Test vergleichen wollen und davon ausgehen, dass wir an einer Effektstärke von 0,5 mit einem Signifikanzniveau von 0,05 interessiert sind, mindestens 64 Beobachtungen in jeder Studiengruppe vorhanden sein, damit die Teststärke 0,8 beträgt.

Tabelle 1. Leistungsanalyse des t-Tests für zwei unabhängige Stichproben

Abbildung 2: Diagramm, das das Verhältnis Stichprobengröße/Power für den t-Test für unabhängige Stichproben mit einem Signifikanzniveau von 0,05 und einer Effektstärke von 0,5 zeigt

Zusammenfassend lässt sich sagen, dass zur Bestimmung der Aussagekraft eines Tests einer der oben genannten Parameter zusammen mit drei weiteren Parametern geschätzt werden muss. So kann die Aussagekraft eines Tests beispielsweise unter Berücksichtigung der Stärke des Effekts, des Stichprobenumfangs und des Signifikanzniveaus geschätzt werden. Die Power-Analyse wird in der Regel vor der Durchführung einer Studie durchgeführt und kann auch a priori verwendet werden, um einen der vier Parameter zu schätzen.