THE THREE-SIGMA RULE

By RAFAŁ WAŚKO (Predictive Solutions)

The three-sigma rule is an important tool in statistics and quality management. In the context of data analysis, it allows the identification of outlier points that are significantly different from the rest of the data. The use of the three sigma rule in quality control also reveals anomalies, allowing early detection of problems and effective response to them, which can help avoid further complications.

WHAT IS SIGMA?

To begin with, it is worth explaining what “sigma” is in statistics. In statistics, the Greek letter “σ” (sigma) is used as a designation for standard deviation. It is a measure of the dispersion of data around the mean. In simple terms, it defines how much the values in a variable differ from the mean value. The greater the value of the standard deviation, the greater the variability in the data. In practice, the standard deviation is an extremely important measure because it allows us to assess how much variation there typically is between individual observation values and the mean. This allows us to determine whether the data is close to the mean (smaller standard deviation) or has greater variation around the mean (larger standard deviation).

ASSUMPTIONS OF THE THREE SIGMA RULE

Before we get to the assumptions, it is worth briefly explaining what a normal distribution is. The history of the three sigma rule begins with work on the normal distribution. This distribution describes the characteristic properties of many natural phenomena, such as physical measurements, test results and many others. The normal distribution is bell-shaped, and most data cluster around a mean value, with decreasing frequency of deviation from the mean.

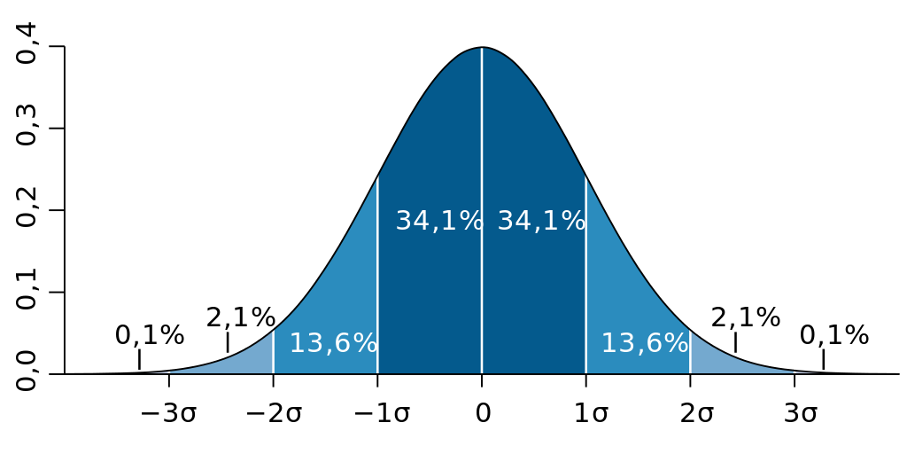
The three sigma rule is based on the assumption that for a normal distribution:

About 68.27% of observations are within one standard deviation (σ) of the mean (μ).
About 95.45% of observations are within two standard deviations of the mean.
About 99.73% of observations are within three standard deviations of the mean.

Figure 1. Normal distribution with individual intervals of one standard deviation wide Source: https://en.wikipedia.org/wiki/Standard_deviation

In short, the three sigma rule, in the case of a normal distribution, indicates that the vast majority of observations (99.73%) fall between three standard deviations below the mean and three standard deviations above the mean. The remainder of the data, representing only 0.27%, can be considered a deviation from the norm. However, it is worth noting that the three sigma rule is based on the assumption that the data have a normal distribution. In practice, many phenomena may have different distributions, so the application of this rule should be preceded by an analysis of the distribution of the data and an assessment of whether this assumption is met.

APPLICATION OF THE THREE-SIGMA RULE

The rule presented in this text can be applied in a variety of fields, such as manufacturing, finance, medicine or social sciences. In manufacturing quality control, it can often be used to monitor production processes and identify potential problems or deviations from the norm. If the data exceeds three sigma from the mean, it can indicate problems in the production process. A second, exemplary area of application is the medical field. In medical data analysis, the three-sigma rule can help identify cases or patient outcomes that differ from the average and may require special attention. Another area could be social research, where the three-sigma rule can be used to identify non-standard behavior or events that may require further analysis.

USING THE THREE-SIGMA RULE IN QUALITY CONTROL AND CONTROL CHARTS

In the early 20th century, Walter A. Shewhart, one of the pioneers in the field of production management processes, began to use statistical methods for quality control in production processes. W. A. Shewhart was one of the creators of control charts, which make it possible to monitor production processes and detect deviations from the standard.

One of W. A. Shewhart’s key achievements was the application of the three sigma rule in quality control. He introduced the concept of control limits, which were multiples of the standard deviation and were used to determine when a process showed irregularities. In control charts, the three-sigma rule is used to monitor the stability of a process and keep it within acceptable variability. Control limits based on this rule define the range within which the process should operate. Points outside the three-sigma boundaries can indicate potential deviations from the norm, requiring further analysis or corrective action.

Analysis of control charts using the three-sigma rule can proceed as follows:

Inside 1σ: if most points are within +/-1σ of the mean, the process is stable and controlled,
Between 1σ and 2σ: if some points are between +/-1σ and +/-2σ, the process can still be controlled, but the variability may be slightly higher,
Between 2σ and 3σ: if the points are between +/-2σ and +/-3σ, the process may require some analysis, but may be acceptable,
Beyond 3σ: if the points go beyond +/-3σ, it may indicate a serious deviation from the norm and the need for corrective action in the process.

Figure 2. An example of a control chart prepared in PS IMAGO PRO. UCL and LCL are values that delineate the empirical 3-sigma area above and below the average measurement value

A key feature of the three-sigma rule is its ability to quickly detect deviations from the norm and enable intervention to bring the process back into a controlled framework. By identifying problems and taking corrective action, it is possible to maintain the quality of processes and products. In this way, the tool assists companies in monitoring, improving quality and effectively managing quality in various areas of operations.

SUMMARY

The history and genesis of the three-sigma rule dates back to work on the normal distribution and quality control. These assumptions have evolved with the advancement of statistics, becoming an integral tool in data analysis, quality control and manufacturing process improvement. With the three-sigma rule, it is possible to quickly detect deviations from the standard and take corrective action to ensure compliance with quality requirements. Finally, it is also worth noting that the three-sigma rule, despite its effectiveness in identifying deviations from the standard, has certain limitations that must be taken into account when applying it. One of the key ones is meeting the assumption of normality of distribution. In practice, data can have different distributions, which can affect the effectiveness of the rule. Therefore, it is important to verify that the data actually meet this assumption. It is also worth remembering that the three-sigma rule identifies deviations outside the three-sigma limits as potential problems. However, not all deviations outside this range are equally significant. A point just outside the three-sigma boundary is treated the same as a point much further away. This limitation can lead to overreaction to random changes. It is important to understand the context, analyze the data carefully and verify assumptions in order to use this tool effectively in practice.